Background
While autonomous vehicles will share the road with human drivers for the foreseeable future, once the road transitions fully to computer drivers, new possibilities will emerge for solving transit problems. A prime example of this is intersection design. The current convention is to block out approximately 30 to 90 seconds during which only cars on certain lanes are allowed to cross. But this approach can be inefficient. We all know the feeling of sitting at a completely empty intersection waiting for an eternal red light to change. In an autonomous future, the intersection computer could know of all approaching vehicles and could stop or allow each to cross in the most efficient order possible. Such complex decisions will require efficient algorithms.
A 2016 paper by Juan José Besa Vial, William E. Devanny, David Eppstein, and Michael T. Goodrich of U.C. Irvine discusses algorithms that can determine the most efficient schedule (i.e. order) for platoons (one or more vehicle travelling as a close group) approaching from different directions to cross an intersection.
Their goal is to find the order that results in the smallest maximum vehicle delay. Previous related work had focused on minimizing the total number of stops or total delay of all vehicles. The authors do not explain why they chose this goal, but they might wish for all platoons to be satisfied with the delay they experience.
The authors model each platoon on each lane by defining a time that it will begin to cross the intersection if it is not delayed ("release time") and the time that it will finish crossing the intersection ("end time"). The length of the platoon is the difference between the release time and the end time. Also, the delay of a platoon is the difference between the release time of a platoon and the time it actually begins to cross.
To further limit the difficulty of the problem, the authors specify that platoons cannot be broken up and that platoons cannot travel backwards. Finally, they only consider one intersection at a time, not interactions between multiple intersections.
Paper: Scheduling Autonomous Vehicle Platoons Through an Unregulated IntersectionIllustration of Intersection Model
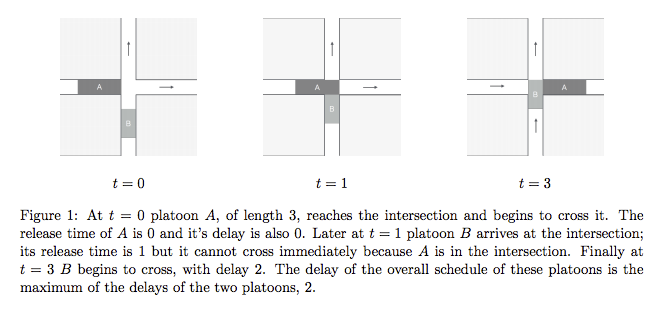
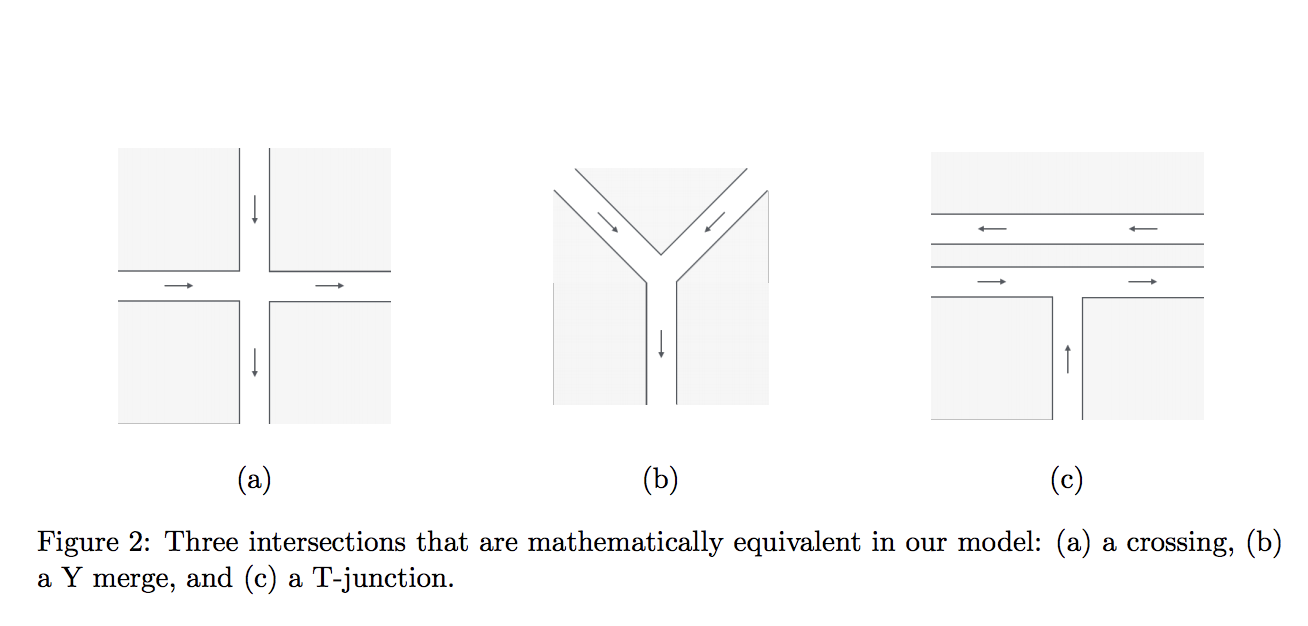
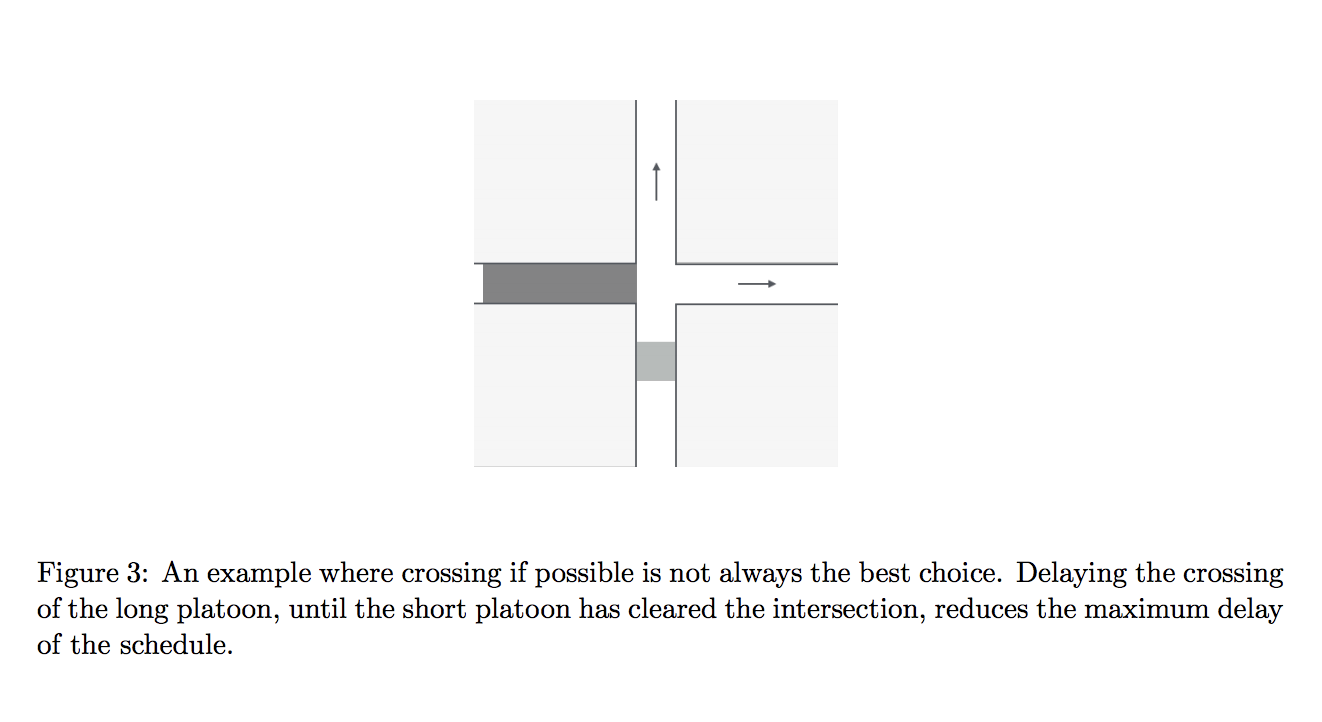
Illustrations source: Vial et al. paper pages 4 & 6.
The Algorithm
The paper’s authors consider several situations: where two lanes merge, where a constant number k lanes merge, and a more complicated scenario involving crossing traffic plus the merge of an arbitrary number of lanes.
For a two-way merge, they find that a simple greedy algorithm can be used. For the crossing with an arbitrary number of merges, the problem is NP-hard. However, for a k-way merge where k is constant, a solution can be found in polynomial time. I implement this algorithm, which is described in section 3.3 of the paper.
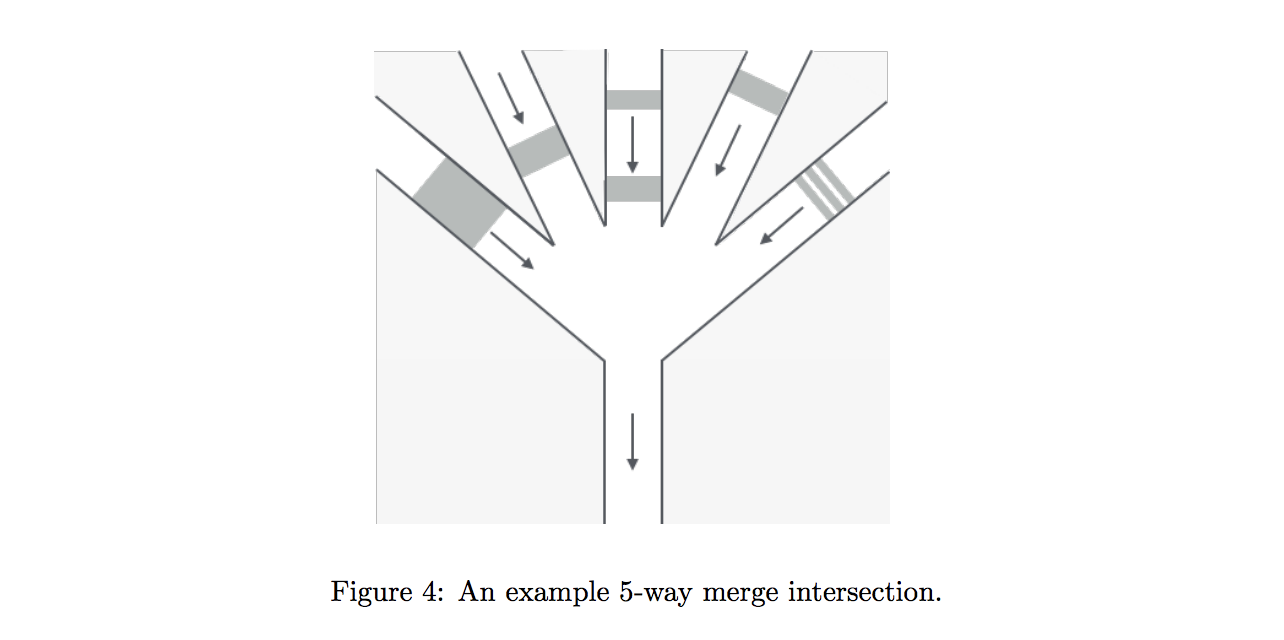
Further, the paper’s authors show in section 3.1 that each optimization algorithm can be derived from a decision algorithm using a parametric search technique from Megiddo. I will focus on the decision algorithm portion, which answers whether or not a schedule exists whereby all platoons can cross the intersection without any platoons being delayed by more than some amount (parameter d).
For this k-way (constant k) decision algorithm, we model the intersection as a series of states. In each state, some number of platoons from each lane has crossed and some number has not yet crossed. For simplicity, no platoons have partially crossed the intersection. We then determine for each state the earliest time that we could reach that state (td(s)). If we cannot reach the state without incurring more than delay of d, then the td(s) of that state is returned as infinite.
Since the time to reach each state relies on the time to reach the states immediately preceding it, the td(s) of each proceeding state is a subproblem, and we can use dynamic programming to find the td(s) of each state. That is, we start with the td(s) of earliest state (where no platoons have crossed) and then allow platoons from each lane to cross one by one in order to find the td(s) of each successor state.
The algorithm functions as follows: for each state s, we find all of its proceeding states si...sk by simply reversing the crossing of a platoon from each lane k, one by one. As such, the number of proceeding states is equal to or less than the number of lanes. For each proceeding state si, we look up td(si) in our dynamic programming table, and then see what the td(s) of our current state would be if we used that proceeding state and allowed the platoon from that lane to cross to bring us to the current state.
Another way to state this it is that each of the most recent platoons to arrives in current state s crossed at the maximum of its original release time and the td(si) of preceeding state si. We then calculate the delay of that platoon by comparing its crossing time to its original release time. Using this approach, we can report whether or not it is possible to reach state s without incurring delay of d. Further, we can calculate td(s) by choosing the preceding state that results in us reaching state s as soon as possible.
We loop through each state until we reach the final state in which all platoons have crossed. There are O(nk) states and finding the td(s) of each state takes constant time, so the algorithm takes O(nk) time in total.